Posts Tagged ‘velocidade’
Ciclocomputador e RPM
Velochinas
De uns anos para cá, com a forte presença industrial chinesa e a natural redução de custo de tecnologias, equipamentos eletrônicos tornaram-se populares e baratos.
Velocímetros (aqui vamos falar dos eletrônicos, pois os mecânicos são divertidos mas pouco funcionais) ou ciclocomputadores são exemplo disso. Além de mais fáceis de encontrar, seu preço foi reduzido em uns 80%. O que antes era um artigo de luxo hoje é apenas mais uma bugiganga.
A tendência é, inclusive, esperar que estes dispositivos com sensores magnéticos no garfo e na roda da bicicleta sejam substituídos integralmente por sistemas baseados em gps. Embora pareça usar um helicóptero para atravessar a rua, qualquer smartphone já é capaz disso.
E os RPM?
Medir velocidade e distância é útil para diversão e referenciamento de mapas / planilhas de navegação. Porém, ao falar de treino físico, essas medidas podem ser enganosas e pouco úteis. Lembre se que 30km/h pode ser pouca velocidade com um vento a favor de 10km/h e muita velocidade caso esse vento seja contra.
Como em um carro de corrida, onde a informação mais importante é a rotação do motor, no ciclismo a medida de esforço do atleta é o que merece destaque. Este parâmetro é dado por um infinidade de valores que podem, de maneira simplificada, ser traduzidos por BPM do coração e RPM da pedivela. O primeiro situa a proporção de quanto seu corpo está gastando de energia e o segundo mostra a se a pedalada está está na faixa biomecânica eficiente. Lembrando que no conceito de ciclismo moderno 80% é preparo físico e 20% é estar na marcha correta (por isso cassetes de 11 engrenagens).
RPM x Ciclocomputador x Preços Abusivos
Monitores cardíacos para BPM seguiram a evolução da eletrônica e ficaram mais acessíveis. Já os ciclocomputadores com sensores de cadência (RPM da pedivela) ainda continuam num nicho de equipamento de performance, custando algo ainda que tenha embarcada a mesma tecnologia de um velocímetro de 3 dólares. Versões genéricas são raras e os de marcas tradicionais custam fábulas (umas 10 vezes mais que um ciclocomputador sem sensor de cadência).
Fazendo sensor de cadência na mão
Uma solução de baixo custo pode ser feita usando matemática e algumas conversões de unidade. O resultado é a possibilidade de usar um ciclocomputador barato exclusivamente para informar a RPM da pedivela.
Para isso, coloca-se um imã na pedivela e o sensor próximo a esta.

Pra quem gastar uma nota se aquele seu velocímetro encostado pode muito bem virar um medidor de RPM?
Parte-se do principio temos uma “roda imaginária” em uma Penny Farthing cuja velocidade seja 100km/h quando se estiver a 100RPM. Algumas contas e chegamos a uma roda cujo perímetro é de 16,666 metros. Praticamente nenhum velocímetro permite setar um perímetro tão grande. Então temos algumas alternativas:
- Caso o velocímetro mostre uma casa decimal, pode-se setar 1,667 metros ao invés de 16,667 metros. Porém aparecerá um valor 10 vezes menor. 100RPM no visor irá aparecer 10,0. Mas é fácil de se acostumar.
- Mais imãs. Uma solução interessante é grudar um imã em cada parafuso da coroa da pedivela (5 nas speed e 4 nas mtb, em geral). Na hora de setar o “perímetro”, divide 16,667 pelo número de imãs. Por exemplo numa speed com 5 parafusos, basta setar 16,667/5=3,333 . Este valor usualmente já é possível inserir como perímetro da roda.
E pronto. Seu mostrador de RPM estará montado e funcionando, com a vantagem de ter um mostrador grande e exclusivo, ótimo para treinos.
Potência e Energia
Ao contrário do que escutamos das diversas vertentes esotéricas, energia é uma grandeza física bastante conhecida. Mensurável, armazenável e principalmente transformável entre sua grande variedade de forma (elétrica, mecânica, gravitacional, química, potencial de mola, pressão de gases, térmica, etc*).
Matematicamente é comum simplificar afirmando que energia é potência integrada na variável tempo ou que potência é a derivada temporal da energia. Simplificando +: para uma potência constante temos que a energia é a multiplicação direta da potência pelo tempo. Ou seja, 1kW (potência) multiplicado por uma hora (tempo) é equivalente a 1kWh (energia), como vemos na conta de luz.
No tópico anterior vimos como as forças resistivas se comportam com a velocidade; se multiplicadas pela velocidade resultam na grandeza potência. Nesta abordagem veremos sua consequência na energia total gasta.
Força de resistência a rolagem
A força de resistência a rolagem possui um comportamento quase constante com a velocidade. Sendo assim, ela não se altera com a velocidade. Vamos tomar dois casos como exemplo:
| CASO A | CASO B | |||
|---|---|---|---|---|
| Força resistiva | 10N | 10N | ||
| Velocidade | 10 m/s | 20 m/s |
A potência (P) é:

Onde:
F = Força
v = Velocidade
Desta forma para vencer a força de resistência a rolagem a 20m/s, a potência dissipada é o dobro (20m/s x 10N = 200W)[Caso A] que a 10m/s (10m/s x 10N = 100W)[Caso B]. Usando um trajeto hipotético com 20m de distância rolando a 20m/s, iremos levar 1 segundo. E a 10m/s, levaremos 2 segundos. Quando consideramos a energia (E) gasta no trajeto total temos:
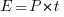
Onde:
E = Energia
t = Tempo
Calculando para cada um dos casos:
Caso A 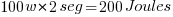
Caso B 
Ou seja, a resistência a rolagem dissipará a mesma energia sempre, independente da velocidade.
E a resistência aerodinâmica?
A resistência aerodinâmica, por sua vez, não possui um comportamento constante com a velocidade. A força de arrasto aerodinâmico é função da velocidade ao quadrado e a potência (força x velocidade) será função da velocidade ao cubo. Para nosso caso hipotético de resistência aerodinâmica de 10N a 10m/s, dissiparíamos 100W. A 20m/s (10 m/s x 2), entretanto, teríamos 40N (10N x 2²) e a potência dissipada seria de 800W (100W x 2³).
Se pensarmos num trajeto hipotético com 20m de distância, teremos que a 20m/s iremos levar 1 segundo. E a 10m/s, levaremos 2 segundos. Quando consideramos a energia gasta no trajeto total temos:
Caso A 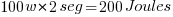
Caso B 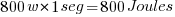
Ou seja, a resistência aerodinâmica dissipará 4 vezes mais energia para cada vez que dobrar a velocidade. A proporção será sempre quadrática.
Ao aumentar a velocidade em 50%, teremos (1,5)²= 2,25 logo gastaremos 225% a mais de energia gasta. E assim por diante.
Não devemos esquecer que a energia dissipada total será a soma destas duas componentes (e dividida pela eficiência total da transmissão, que é em torno de 90% ou 0,9))
No nosso exemplo da bicicleta é bastante difícil medir a energia gasta. Mas como a lei da física vale para todos os veículos, vemos o mesmo fenômeno nos carros. E nos carros é bastante fácil de medir pelo combustível, que nada mais é que energia. Verifica-se que é gasto no mesmo trajeto, aproximadamente o dobro do combustível andando a 120km/h que a 80km/h (a quatrorodas comprovou isso aqui).
Academias podiam ser um pouco mais úteis para humanidade
Para se pedalar a 20km/h gasta-se aproximadamente 150W. A energia total média consumida dividida pelo tempo, para uma casa brasileira de 3 pessoas é 150W também. Ou seja, se cada uma das pessoas da casa pedalasse um gerador por 8 horas, esta casa poderia ser autossuficiente energeticamente. É uma ideia ridícula, mas podemos pensar que academias com centenas de alunos poderiam ser pequenas usinas.
Um comentário final
Na física todas as formas de energia podem ser, na sua análise mais profunda, descritas pelas forças Fraca, Forte, Eletromagnética e gravitacional. No dia a dia, apenas eletromagnética e gravitacional. Por exemplo uma reação química não subatômica é composta por fenômenos eletromagnéticos entre os átomos.
Força e Potência
Para pedalar mais rápido – o dobro da velocidade atual, será que você precisa:
- dobrar também a potência atual;
- triplicar a potência atual;
- quadruplicar a potência atual;
- desistir disso.
A única resposta aceitável é desistir, mas a correta mesmo é o tema desse post.
Teoria
Praticamente todas as máquinas usadas como meios de transporte encontradas são consideradas, segundo a física, como corpos sólidos se deslocando em meios fluídos. Neste sistema temos a entrada de potência que se equilibra com a potência perdida (dissipada) quando se encontra numa trajetória plana e em velocidade constante. Usualmente toda potência perdida é na realidade transformada em calor.
Esta potência dissipada ocorrerá de 3 formas:
- arraste viscoso;
- resistência a rolagem e;
- perdas na transmissão – uma forma de arraste viscoso e atrito.
As perdas na transmissão em geral são representadas por %, tendendo a serem aproximadas por constantes. Ex. um mecanismo com 15% de perda, reduzirá 1,5cv num sistema que introduz 10cv ou 15cv num sistema que introduz 100cv.
A resistência a rolagem, em geral constituída pelo atrito dos pneus com o solo – e deformações do pneu – possui um comportamento aproximadamente constante. Ex. uma roda que reage com uma força de 10N no sentido contrário ao movimento a 15m/s, também resistirá com 10N caso a velocidade seja 5m/s. Entretanto a potência é o produto de força x velocidade. Por isso embora a força nas duas velocidades seja a mesma, para 15m/s teremos 150W dissipados enquanto que a 5m/s teremos apenas 50W. Obviamente em máquinas voadoras e aquáticas não temos esta componente da perdas.
Em velocidades proporcionalmente baixas, resistência a rolagem e perdas mecânicas são predominantes – num trator por exemplo. Em outros casos o arraste viscoso é o mais perceptível, como em uma bicicleta com pneus finos onde as perdas na transmissão são da ordem de apenas 4% e os pneus finos de alta pressão (8 Bar) reduzem ao máximo a resistência a rolagem.
O arraste viscoso se deve ao deslocamento do corpo no fluído. Da mesma forma que uma pedra cai mais lentamente quando dentro da água ou quando um papel amassado cai mais rápido que uma folha plana. Trata se do cisalhamento de infinitas camadas do fluído somadas com descolamentos e vórtices. Na prática simplificamos, para os meios de transporte, com:
- Constantes do fluido (K): onde se inclui viscosidade, massa específica, etc.
- Constantes geométricas: forma (traduzida pelo Cd.) e área frontal
- Fator dinâmico: simplificando, velocidade ao quadrado(v².).
E alguns cálculos
Apenas conceitualmente podemos caracterizar a força do arraste viscoso como porcentagem:

As constantes não mudam com a velocidade nesta simplificação. Logo temos o comportamento quadrático da força com a velocidade. Por exemplo, andando a 5m/s temos 10N de arraste viscoso. Dobrando a velocidade, temos 4 vezes mais arraste viscoso, ou seja, para 10m/s temos 40N de arraste.
Entretanto esta relação fica ainda mais acentuada quando se pensa em potência (P). Como potência é Força x Velocidade, temos para o arraste viscoso:

Resumindo, temos a proporção de:

Ou seja, para cada vez que se dobra a velocidade, precisa-se de 8 vezes mais potência.
Por isso um carro com 125cv que consegue chegar a 200km/h precisaria de 1000cv (oito vezes mais) para atingir 400km/h (duas vezes mais).
Ou exemplo mais prático é que aproximadamente qualquer qualquer pessoa consegue pedalar a 25km/h no plano (algo em torno de 150w).
Porém para se manter 50km/h precisa de potência praticamente fora da capacidade de um humano comum (1200w).

