Archive for setembro, 2009
Raios que o partam
Aros raiados são uma das construções mais leves e resistentes da mecânica. Um aro de bicicleta convencional suporta facilmente 500kgf em carregamento estático e lateralmente mais de 50kgf. Um aro construido com bons materiais e raios de boa qualidade dificilmente irá estragar, exceto por fadiga dos raios onde eles prendem no cubo ou por algum abuso do ciclista.
Seu conceito é uma treliça 3D onde os raios sofrem tração entre o cubo e o aro. Considerando cada extremidade de cada raio como um ponto, ao ligarmos estes pontos teremos uma estrutura composta por inúmeros tetraedros.
Vamos citar algumas observações interessantes:
1: Os Niples que fazem o ajuste da tensão a conexão entre o aro e o raio são apenas apoiados. Ou seja, se empurrar um raio solto no sentido do pneu faz ele sair. Os niples apenas permitem a tração dos raios.
2: O ponto de contado do raio com o cubo não é engastado, ou seja, permite 2 graus de liberdade ( como se fosse uma articulação).
3: Os raios, apesar de parecerem rigidos, para a ordem de grandeza dos esforços eles se comportam flexivelmente ( como se fosse um cabo de aço). Inclusive o indice de esbeltez ( comprimento dividido pelo diâmetro) é superior a 200, por isso não possui rigidez para compressão sem que haja flambagem.
Mesmo com estas características, a sistema todo se comporta como uma estrutura rígida ( desconsiderando as deformações nos elementos). De maneira simplificada, poderiamos subistituir os raios por cabos de aço que ela resistiria da mesma forma.
A distribuição de forças se da seguinte forma ( figura 1). Supondo o carregamento no cubo ( força para baixo), o cubo fica “pendurado” nos raios superiores (figura 1A). Porém se só existissem estes raios, facilmente deformaria o aro.
O mesmo aconteceria se só existissem os raios laterais ( figura 1B). O mínimo necessário para suportar é a composição de raios laterais e superiores, sendo que os superiores “penduram” o cubo e os laterais ajudam a manter a intregridade da roda(figura 1C). Obviamente isto é uma abstração momentanea, uma vez que a roda pode girar, deixando de ter sentido as palavras “superiores” e “laterais”.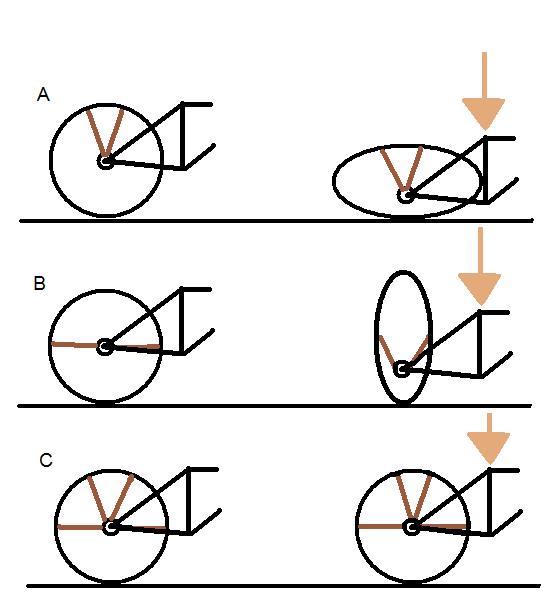
Mas E OS RAIOS DE BAIXO?
Quando os raios estão na parte inferior da roda, pouco ou nenhuma contribuição dão para a sustentação, ao contrario do que a intuição visual nos faz acreditar. Como ja foi dito, eles não resistem a compressão.
Podemos estender estas considerações a qualquer roda raiada, desde motos até rodas de aviões (desde a época do 14bis!).
Rodas maçiças como as de carros atuais ou as rodas de 3 ou 4 raios de material composito funcionam com outros conceitos, praticamente apenas calculáveis com modelos númericos de elementos finitos ( CAE).
Material bike
Podemos considerar relativamente simples a construção dos quadros, sendo constituídos, em maioria, de tubos cilíndricos soldados e calandrados, excetuando-se apenas aqueles sem solda e os de fibra de carbono (mais recentes; moldados no formato definitivo).
Em uma publicação futura será dada a devida atenção ao processo de fabricação. Nesta apenas iremos abordar sobre os possíveis materiais usados nas bicicletas.
Especificações
Para compará-los existem diversos aspectos, entre eles: sensibilidade ao entalhe, KiC, resistência à abrasão, à corrosão, entre muitas outras possibilidades. Porém como se trata de um veículo que utiliza uma quantia de potência muito baixa, o peso acaba sendo um parâmetro muito adequado.
Isoladamente, o peso ( representado pela densidade; massa /volume), não representa muita informação. Quanto atrelado à resistência à tração (força/área), é possível gerar um só número de resistência e massa, elaborando um indicador justo para avaliação de materiais.
A resistência máxima a tração é representada usualmente pela unidade Mpa (Mega Pascal) e corresponde a quantos N (Newtons) um milimetro quadrado suporta.
A densidade será representada por Mg/m³ , ou toneladas por metro cúbico. O novo valor será dado por Mpa/(Mg/m³) e corresponde a uma resistência específica, ou seja, quanto uma massa deste material consegue suportar de força.
Os Materiais
- Aço ao carbono (Aisi 1020). Das antigas bicicletas de estrada de 10 marchas até “bicicletas de supermercado” da atualidade.
- Cromo Molibdênio Cr-Mo (Aisi 4340) . As chamadas “de cromo”, presentes há alguns anos atrás, porém rarissímas de serem encotradas novas.
- Alumínio 6061 e alumínio 7075. Chamadas de ligas aeronáuticas, vão de ligas fáceis de soldar e baratas como o 6061 até as carissímas 7075, também chamadas de Scandium.
- Magnésio (ZK60A). Preços estratosféricos. No Brasil são impossíveis de achar a pronta entrega.
- Titânio. Pode ter várias ligas, porém iremos arbitrar que se trata da T1-13 V-11 Cr-3 Al, já que os fabricantes não divulgam qual é a correta.
- Fibra de carbono. Modernos, caros e com propriedades que dependem muito dos processos de fabricação (moldagem e cura), pouco padronizados até o momento.
| Material | Res. Tração |
Densidade |
Res. Específica |
| Aço 1020 | 379 | 7,8 | 48,59 |
| Aço 4340 | 1700 | 7,8 | 217,95 |
| Alumínio 6061 | 276 | 2,8 | 98,57 |
| Alumínio 7075 | 503 | 2,8 | 179,64 |
| Magnésio | 365 | 1,8 | 202,78 |
| Titânio | 1241 | 4,4 | 282,05 |
| Fibra de Carbono | 3900 | 1,7 | 2294,12 |
Estes valores explicam a predominância de quadros de fibra de carbono em bicicletas de competição . Obviamente, na prática, os valores são inferiores pela da perda parcial de alguns tratamentos térmicos no processo de soldagem.
Também não se pode confiar 100% que as ligas descritas pelos fabricantes são exatamente as mesmas que eles utilizam na fabricação, principalemente com a presença de inúmeros fabricantes genéricos chineses nas bicicletarias.
Tubos
É muito fácil estimar a idade de uma bicicleta. Mesmo de longe, mesmo sem ver os componentes, podemos dar um palpite sobre época em que ela foi fabricada olhando apenas as espessuras dos tubos que compõe o quadro.
Nos anos dourados das bicicletas de 10 marchas ( 2×5) os tubos eram muito finos, feitos de aço ao carbono (provavelmente da ordem dos AISI 1020).

Uns 10 anos depois entravam em cena as primeiras bicicletas todo-terreno de alto nível, estreando materiais novos como o aço liga de Cr-Mo ( cromo e molibdêmio) e paralelamente a isso tinhamos avanços na geometria, com tubos ligeiramente maiores ( maior diâmetro)
Com a entrada do alumínio na construção de bicicletas, material de propriedades muito diferentes do aço (baixo peso porém baixa resistência a tração e baixo módulo de elasticidade, ou seja, mais mole e menos resitente) as dimensões usuais dos tubos tiveram que ser revistas.

Os tubos de um quadro praticamente só sofrem dois tipos de esforços:
Flexão, quando se pedala de pé e “torce ” a bicicleta.
Tração e compressão. Tratando o quadro como uma treliça, vemos que alguns tubos são “puxados” e outros apertados.
A tração e compressão em tubos de aluminio pode ser facilmente compensada se utilizar tubos com espessura maior, ou seja, aumentando a área transversal temos mais material para aguentar o esforço.
A resistência a flexão , entretanto, não tem um comportamento proporcional com a área transversal. Ela se relaciona com um termo conhecido pelo simbolo Ix ou Iy ou Iz cuja fórmula é dada, para o caso específico de tubos cilindricos por:
Ix= pi * ( D² + d²)*(d²-d²)/4 onde D é o diâmetro externo e d é o diâmentro interno e pode ser simplificada para
Ix= pi/4* (D^4-d^4)
Ou seja, é mais vantajoso, para melhorar o comportamento para a flexão usar tubos de baixa espessura porêm de diâmetros grandes ao invés de tubos finos e espessos.
No exemplo da figura 3 temos 2 tubos vistos de frente. Ambos possuem a mesma área transversal, ou seja pesariam exatamente o mesmo se tivessem o mesmo comprimento e teriam a mesma quantidade de material. A única diferença entre eles é a espessura e o diâmetro.
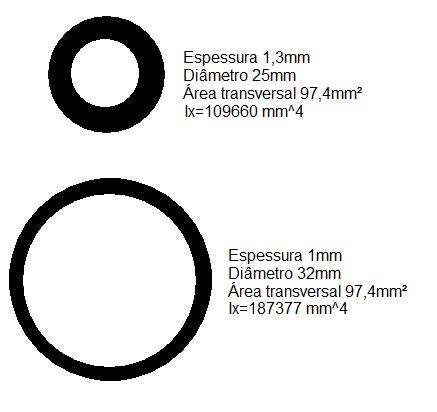
Pode-se ver pelo valor calculado para o Ix, que o tubo de diâmetro maior e menor espessura possui quase 80% maior resistência a flexão que o tubo mais fino.
Porém não podemos reduzir muito a espessura do tubo, pois isso deixaria ele sensível demais a pequenos impactos laterais ( pedras, batidas da corrente).
Faca no Dentes
Quem pedala, mesmo que muito pouco já sabe que “quanto mais dentes atrás ( cassete) mais leve fica para pedalar” e que “quanto mais dentes na frente ( pedivela) mas pesada fica para pedalar”
Sabemos também que a velocidade é inversamente proporcional ao torque produzido na roda, ou seja, precisando de força numa subida usamos marchas curtas ( sinônimo de marchas leves, reduzidas, etc) e precisando de velocidade num plano usamos marchas longas.
Nesta postagem será dado um enfoque para a força na pedivela , na corrente, no cassete e na roda, tentando mostrar como eles se relacionam.
Vamos começar com um exemplo familiar (de familia mesmo). Imagine 2 pessoas brincando numa gangorra num parquinho. Se ambas pesarem 60 Kgf , basta que se sentem a mesma distância em relação ao eixo da balança para que as forças fiquem equilibradas por somatório de momentos.
Porém , caso uma das pessoas tenha uma massa menor, e consequentemente exerça menos força, não é possivel equilibrar a gangorra mantendo as mesmas distâncias do centro como pode ser visto na figura 1.
Como o momento sobre um ponto é dado por: F . d = M
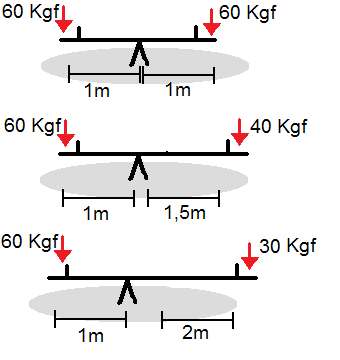
E também por ser necessário, para manter o equilíbrio, que a soma dos momentos em torno no eixo de apoio seja igual a zero, temos para o caso 1:
60 Kgf x 1m + 60 Kgf x (-1)m =0 sendo que o sinal negativo mostra quem esta a esquerda do eixo em relação a horizontal.
Para o caso 2 e 3:
40 x 1,5 +60 x (-1) = 0
e
30 x 2 + 60 x (-1) =0
Resumidamente, quanto mais afastada do centro menor é a força, desde que se esteja em equilíbrio.
Se considerarmos uma pedivela como um tipo de gangorra ( alavanca) onde o movimento central é ponto de apoio e as extremidades da alavanca são os pedais e o ponto onde o primeiro dente da pedivela toca a corrente, podemos fazer uma analogia,vejamos a figura 2.
Supomos 3 coroas de diferentes tamanhos ( 28, 38, 48 dentes) e uma pessoa aplicando força sobre um dos pedais quando o braço da pedivela esta paralelo ao chão. Neste exato instante temos a mesma situação da gangorra, mudando apenas os valores das forças e das distâncias entre a aplicação da força e o ponto de apoio. Note que a força realizada pela corrente é igual a tração que ela sofre e atinge valores razoavelmente altos.
Assim pode-se perceber por que quanto mais dentes na pedivela ( e consequentemente maior distância entre eixo e ponto de aplicação de força pela corrente), menor a tração na corrente. Resumindo, podemos dizer que para produzir a mesma tração na corrente que a coroa menor produz, temos que fazer muita força se usar a coroa maior.
O mesmo raciocinio pode ser aplicado na roda traseira. Neste caso temos como força, além da tração na corrente atuando no cassete, temos a força de atrito na roda, ou seja, a força que “empurra” a bicicleta de fato. O eixo de apoio é o próprio eixo do cubo traseiro .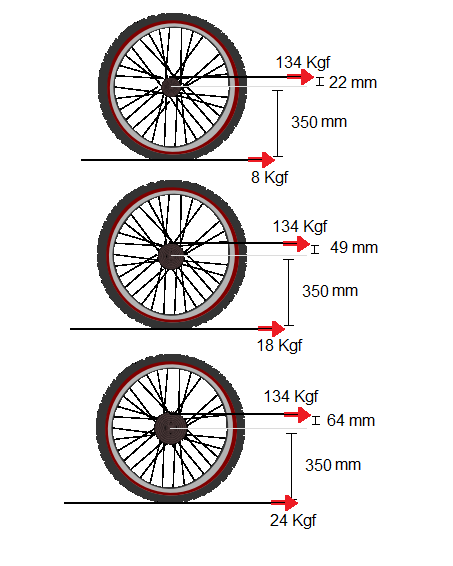
No exemplo da figura 3, utilizamos como tração na corrente o mesmo valor obtido na figura 2 para o uso da coroa intermediária.
Vendo nesta forma fica mais claro perceber por que um número grande de dentes no cassete permite que a roda faça uma força maior .
Obs. As distâncias foram calculadas para cassetes de 32, 25 e 11 dentes e para uma pedivela arbitrária de 48, 38, 28 dentes. O raio da roda ( raio matemático, diâmetro dividido por 2, não a peça metálica) foi medido a partir de uma aro 26″ com pneu 1,25″.
You are currently browsing the garagem do odois blog archives for setembro, 2009.
