garagem do odois

A sensação de “dureza” ou “moleza” de qualquer coisa depende, de forma simplificada, da rigidez do elemento que está se deformando e da quantidade deste elemento que está sujeita a força. Na prática, a sensação de “dureza” é a proporção da deformação causada por uma força. Quanto mais deformação, mais “mole” tende a parecer.

Deita aqui

Pensando num exemplo mais cotidiano e de mais fácil percepção podemos pensar numa cama com um colchão. Quando se coloca 2 colchões empilhados percebe-se que que este arranjo é muito mais “mole” que quando comparado com apenas um colchão.

Ao deitar-se no colchão, este se deforma 5cm de profundidade; empilhando 2 iguais, como a força é aplicada para os 2, cada um irá deformar 5cm, totalizando 10cm. Como há uma deformação maior para a mesma força, há sensação de que 2 colchões empilhados são mais moles que um só.

Para quem está mais familiarizado com sistemas elétricos, pode pensar que a força é Volts, deformação é Ampere e os colchões empilhados são Resistores em paralelos. A matemática é a mesma.

E o pneu com isso?

Vamos pensar num pneu. O elemento que está se deformando é o ar (diminuindo o espaço vazio entre as moléculas dos gases do ar). A quantidade do elemento é a massa de ar, que será proporcional ao volume do pneu multiplicado pela pressão. No nosso caso, para efeito comparativo, iremos tratar somente de pressões iguais e larguras dos pneus iguais. Assim, temos que a quantidade de ar é proporcional apenas com o volume do pneu.

Como qualquer fluido num volume fechado, o ar exerce uma pressão hidrostática. Ou seja, a pressão em qualquer ponto do volume é a mesma. Quando se calibra o pneu com 4 Bar, por exemplo, esta pressão será a mesma em qualquer ponto dentro do pneu, (seja em cima ou embaixo*).
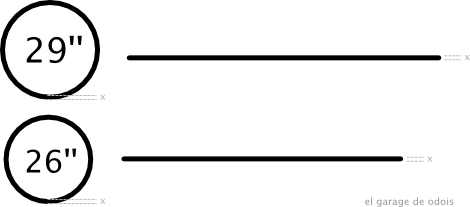
Na nossa comparação teremos um aro 26” e um aro 29” com pneus de igual medida (mesma secção transversal).

Considerando que o volume de ar no pneu é:

volume de ar pneu=secção transversal do pneu x perímetro do aro

E perímetro do aro é :

perímetro do aro = diâmetro do aro x pi

Cancelando os termos iguais , temos que o pneu aro 29” tem 29/26 vezes o volume de ar de um pneu aro 26”, aproximadamente 10% a mais.

Secção transversal igual, pneus diferentes, volumes diferentes

Seguindo a lógica do colchão, o pneu com volume 10% maior irá se deformar 10% mais ao passar num obstáculo (transpor uma pedra a 25km/h, por exemplo). Como amplitude do impacto sentido pelo corpo é:

Amplitude do impacto= altura do obstáculo – deformação do pneu – deformação da suspensão

Temos que o impacto será menor com o aro 29”, resultando em mais conforto.

A curiosidade é que, como a pressão hidrostática se distribui igualmente, caso se ligue um cilindro cheio de ar na válvula do pneu, este pneu com o cilindro conectado tornará o volume total maior, e deixará o pneu mais confortável para a mesma pressão.

A outra curiosidade é o porque pneu maciços são tão inviáveis e desconfortáveis. Como a borracha não é um fluido (sem pressão hidrostática, portanto) toda a força é aplicada apenas no pequeno volume de borracha entre o aro e o solo, ao contrario do pneu de ar, cuja força se distribui por todo o volume de ar no pneu.

Quem já experimentou bicicletas com as mesmas configurações porém com aros diferentes – em geral numa MTB aro 26 é possível colocar um aro 700 com um pneu 23mm, percebe maior suavidade ao experimentar aros maiores, mesmo que se mantenha pneus equivalentes em pressão e largura.

O desconforto ao se deslocar com uma bicicleta num terreno irregular é consequência das variações de nível, resultando em movimento oscilatório para o ciclista. Transpor uma pedra, por exemplo, faz necessário sair do nível do solo e subir até o nível da pedra.

De forma prática pode se dizer que passar por um obstáculo horizontalmente resulta num movimento vertical. Logo, quanto mais rápido se passar pelo obstáculo, mais intenso será o movimento na vertical.

Esse efeito ocorrerá de maneira diferente dependendo do tamanho das rodas. A geometria e a física mostram que para rodas maiores este movimento na vertical será mais lento. Para entender, vamos usar a ilustração abaixo com uma roda idealizada, sem deformação dos pneus nem suspensão:

esquema das trajetórias

Na trajetória descrita pelo centro da roda na primeira roda (linha vermelha) tem-se que, para sair do nível do solo e chegar no obstáculo foi necessário percorrer a distância horizontal de A até C.

Na trajetória da roda menor (linha azul) a distância para esta mudança de nível se deu na distância horizontal menor, de B até C.

Considerando que ambas as rodas estão com a mesma velocidade horizontal, pode se afirmar que a roda menor (azul) irá subir no obstáculo em menor tempo:

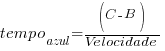
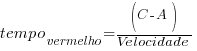
A velocidade vertical (golpe da bicicleta contra o ciclista em função do obstáculo) é a responsável pela sensação de maciez: quanto mais lento, mais macio.

Na situação da roda maior temos a velocidade vertical descrita por:

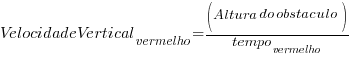
Como a altura do obstáculo é a mesma em ambos os casos, tem se a velocidade maior quando o tempo para subi-lo é menor.

Desta forma pode se ver que quanto menor a roda, maior a velocidade vertical e, portanto, a sensação de impacto.

Na prática pode se verificar isso com as suspensões disponíveis. Aquelas para MTB aro 29 são de curso menor quando comparadas com as MTB aro 26, já que o impacto será menor numa roda maior.