garagem do odois

Velochinas

De uns anos para cá, com a forte presença industrial chinesa e a natural redução de custo de tecnologias, equipamentos eletrônicos tornaram-se populares e baratos.

Velocímetros (aqui vamos falar dos eletrônicos, pois os mecânicos são divertidos mas pouco funcionais) ou ciclocomputadores são exemplo disso. Além de mais fáceis de encontrar, seu preço foi reduzido em uns 80%. O que antes era um artigo de luxo hoje é apenas mais uma bugiganga.

A tendência é, inclusive, esperar que estes dispositivos com sensores magnéticos no garfo e na roda da bicicleta sejam substituídos integralmente por sistemas baseados em gps. Embora pareça usar um helicóptero para atravessar a rua, qualquer smartphone já é capaz disso.

E os RPM?

Medir velocidade e distância é útil para diversão e referenciamento de mapas / planilhas de navegação. Porém, ao falar de treino físico, essas medidas podem ser enganosas e pouco úteis. Lembre se que 30km/h pode ser pouca velocidade com um vento a favor de 10km/h e muita velocidade caso esse vento seja contra.

Como em um carro de corrida, onde a informação mais importante é a rotação do motor, no ciclismo a medida de esforço do atleta é o que merece destaque. Este parâmetro é dado por um infinidade de valores que podem, de maneira simplificada, ser traduzidos por BPM do coração e RPM da pedivela. O primeiro situa a proporção de quanto seu corpo está gastando de energia e o segundo mostra a se a pedalada está está na faixa biomecânica eficiente. Lembrando que no conceito de ciclismo moderno 80% é preparo físico e 20% é estar na marcha correta (por isso cassetes de 11 engrenagens).

RPM x Ciclocomputador x Preços Abusivos

Monitores cardíacos para BPM seguiram a evolução da eletrônica e ficaram mais acessíveis. Já os ciclocomputadores com sensores de cadência (RPM da pedivela) ainda continuam num nicho de equipamento de performance, custando algo ainda que tenha embarcada a mesma tecnologia de um velocímetro de 3 dólares. Versões genéricas são raras e os de marcas tradicionais custam fábulas (umas 10 vezes mais que um ciclocomputador sem sensor de cadência).

Fazendo sensor de cadência na mão

Uma solução de baixo custo pode ser feita usando matemática e algumas conversões de unidade. O resultado é a possibilidade de usar um ciclocomputador barato exclusivamente para informar a RPM da pedivela.

Para isso, coloca-se um imã na pedivela e o sensor próximo a esta.

Pra quem gastar uma nota se aquele seu velocímetro encostado pode muito bem virar um medidor de RPM?

Parte-se do principio temos uma “roda imaginária” em uma Penny Farthing cuja velocidade seja 100km/h quando se estiver a 100RPM. Algumas contas e chegamos a uma roda cujo perímetro é de 16,666 metros. Praticamente nenhum velocímetro permite setar um perímetro tão grande. Então temos algumas alternativas:

1. Caso o velocímetro mostre uma casa decimal, pode-se setar 1,667 metros ao invés de 16,667 metros. Porém aparecerá um valor 10 vezes menor. 100RPM no visor irá aparecer 10,0. Mas é fácil de se acostumar.
2. Mais imãs. Uma solução interessante é grudar um imã em cada parafuso da coroa da pedivela (5 nas speed e 4 nas mtb, em geral). Na hora de setar o “perímetro”, divide 16,667 pelo número de imãs. Por exemplo numa speed com 5 parafusos, basta setar 16,667/5=3,333 . Este valor usualmente já é possível inserir como perímetro da roda.

E pronto. Seu mostrador de RPM estará montado e funcionando, com a vantagem de ter um mostrador grande e exclusivo, ótimo para treinos.

Velocímetro só na aparência. Já é um medidor de RPM.

A sensação de “dureza” ou “moleza” de qualquer coisa depende, de forma simplificada, da rigidez do elemento que está se deformando e da quantidade deste elemento que está sujeita a força. Na prática, a sensação de “dureza” é a proporção da deformação causada por uma força. Quanto mais deformação, mais “mole” tende a parecer.

Deita aqui

Pensando num exemplo mais cotidiano e de mais fácil percepção podemos pensar numa cama com um colchão. Quando se coloca 2 colchões empilhados percebe-se que que este arranjo é muito mais “mole” que quando comparado com apenas um colchão.

Ao deitar-se no colchão, este se deforma 5cm de profundidade; empilhando 2 iguais, como a força é aplicada para os 2, cada um irá deformar 5cm, totalizando 10cm. Como há uma deformação maior para a mesma força, há sensação de que 2 colchões empilhados são mais moles que um só.

Para quem está mais familiarizado com sistemas elétricos, pode pensar que a força é Volts, deformação é Ampere e os colchões empilhados são Resistores em paralelos. A matemática é a mesma.

E o pneu com isso?

Vamos pensar num pneu. O elemento que está se deformando é o ar (diminuindo o espaço vazio entre as moléculas dos gases do ar). A quantidade do elemento é a massa de ar, que será proporcional ao volume do pneu multiplicado pela pressão. No nosso caso, para efeito comparativo, iremos tratar somente de pressões iguais e larguras dos pneus iguais. Assim, temos que a quantidade de ar é proporcional apenas com o volume do pneu.

Como qualquer fluido num volume fechado, o ar exerce uma pressão hidrostática. Ou seja, a pressão em qualquer ponto do volume é a mesma. Quando se calibra o pneu com 4 Bar, por exemplo, esta pressão será a mesma em qualquer ponto dentro do pneu, (seja em cima ou embaixo*).
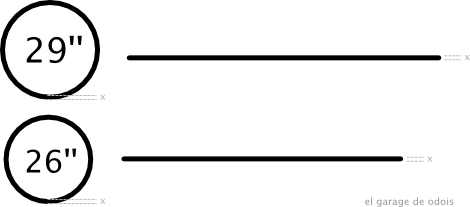
Na nossa comparação teremos um aro 26” e um aro 29” com pneus de igual medida (mesma secção transversal).

Considerando que o volume de ar no pneu é:

volume de ar pneu=secção transversal do pneu x perímetro do aro

E perímetro do aro é :

perímetro do aro = diâmetro do aro x pi

Cancelando os termos iguais , temos que o pneu aro 29” tem 29/26 vezes o volume de ar de um pneu aro 26”, aproximadamente 10% a mais.

Secção transversal igual, pneus diferentes, volumes diferentes

Seguindo a lógica do colchão, o pneu com volume 10% maior irá se deformar 10% mais ao passar num obstáculo (transpor uma pedra a 25km/h, por exemplo). Como amplitude do impacto sentido pelo corpo é:

Amplitude do impacto= altura do obstáculo – deformação do pneu – deformação da suspensão

Temos que o impacto será menor com o aro 29”, resultando em mais conforto.

A curiosidade é que, como a pressão hidrostática se distribui igualmente, caso se ligue um cilindro cheio de ar na válvula do pneu, este pneu com o cilindro conectado tornará o volume total maior, e deixará o pneu mais confortável para a mesma pressão.

A outra curiosidade é o porque pneu maciços são tão inviáveis e desconfortáveis. Como a borracha não é um fluido (sem pressão hidrostática, portanto) toda a força é aplicada apenas no pequeno volume de borracha entre o aro e o solo, ao contrario do pneu de ar, cuja força se distribui por todo o volume de ar no pneu.

Quem já experimentou bicicletas com as mesmas configurações porém com aros diferentes – em geral numa MTB aro 26 é possível colocar um aro 700 com um pneu 23mm, percebe maior suavidade ao experimentar aros maiores, mesmo que se mantenha pneus equivalentes em pressão e largura.

O desconforto ao se deslocar com uma bicicleta num terreno irregular é consequência das variações de nível, resultando em movimento oscilatório para o ciclista. Transpor uma pedra, por exemplo, faz necessário sair do nível do solo e subir até o nível da pedra.

De forma prática pode se dizer que passar por um obstáculo horizontalmente resulta num movimento vertical. Logo, quanto mais rápido se passar pelo obstáculo, mais intenso será o movimento na vertical.

Esse efeito ocorrerá de maneira diferente dependendo do tamanho das rodas. A geometria e a física mostram que para rodas maiores este movimento na vertical será mais lento. Para entender, vamos usar a ilustração abaixo com uma roda idealizada, sem deformação dos pneus nem suspensão:

esquema das trajetórias

Na trajetória descrita pelo centro da roda na primeira roda (linha vermelha) tem-se que, para sair do nível do solo e chegar no obstáculo foi necessário percorrer a distância horizontal de A até C.

Na trajetória da roda menor (linha azul) a distância para esta mudança de nível se deu na distância horizontal menor, de B até C.

Considerando que ambas as rodas estão com a mesma velocidade horizontal, pode se afirmar que a roda menor (azul) irá subir no obstáculo em menor tempo:

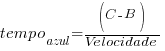
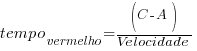
A velocidade vertical (golpe da bicicleta contra o ciclista em função do obstáculo) é a responsável pela sensação de maciez: quanto mais lento, mais macio.

Na situação da roda maior temos a velocidade vertical descrita por:

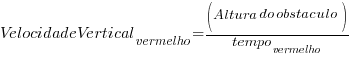
Como a altura do obstáculo é a mesma em ambos os casos, tem se a velocidade maior quando o tempo para subi-lo é menor.

Desta forma pode se ver que quanto menor a roda, maior a velocidade vertical e, portanto, a sensação de impacto.

Na prática pode se verificar isso com as suspensões disponíveis. Aquelas para MTB aro 29 são de curso menor quando comparadas com as MTB aro 26, já que o impacto será menor numa roda maior.

Você já deve ter se perguntado:

Comprimento da pedivela – ou braço de pedivela – é documento?

Teremos que estudar o problema do começo. A locomoção numa bicicleta é essencialmente rotativa. É através do giro das bi – cycle (duas rodas) que temos o movimento desejado. Por simples que pareça, temos aí um problema:

As rodas giram indefinidamente, quantas voltas se possa imaginar, enquanto que nós humanos temos articulações que permitem apenas frações de uma volta – ângulos menores que 360º.

Mecanismo das Quatro Barras

A solução deste problema se dá por via de uma interessante concepção chamada de mecanismo de quatro barras. Através deste curioso arranjo com quatro “links” de diferentes tamanhos é possível transformar movimentos alternativos – que não completam uma volta – em movimentos rotativos – giram indefinidamente -, como é o caso da pedivela – e manivelas em geral. A conversão no sentido contrário também existe, caso dos limpadores de parabrisas de carros.

As medidas de cada uma das barras influi diretamente na velocidade de rotação e no torque. Na situação da bicicleta temos as medidas humanas constituídas pelas pernas compondo duas – uma acima e outra abaixo do joelho – das quatro barras.

A terceira barra seria o braço da pedivela. A quarta barra é onde tudo está fixado ou, geometricamente, a distância da articulação do fêmur na bacia até a caixa central

Clicando na imagem a seguir você pode ver a influência dessas medidas no comportamento do mecanismo por meio de um software.

Clique para ir simular lá no Wolfram

A medida básica para este sistema funcionar é que:

• o comprimento da bacia até o joelho seja maior que a do braço da pedivela e que;
• o comprimento do (selim até caixa central+distância da pedivela) seja menor que o comprimento da perna inteira.

Sem estes não temos a transformação de alternativo em rotativo. Na prática significa que com a perna esticada precisa tocar o pedal na sua posição mais baixa.

Afinal, é ou não é documento?

Existe uma certa expectativa em utilizar pedivelas com braço maior em pessoas maiores. Estes braços são disponíveis em comprimentos que variam de 165 a 177,5mm. Em geral encontramos as opções de 170 ou 175 para componentes mais acessíveis. Podemos fazer algumas considerações de força e torque para uma mesma pessoa utilizando pedivelas de comprimentos diferentes (e todos os demais componentes iguais para cada situação):

Pedivela longa em relação a pedivela curta:

• A perna irá fazer uma força menor para o mesmo torque na roda.
• Como a potência é igual, a perna irá se movimentar mais rápido.
• O ângulo de articulação do joelho e no glúteo será maior durante uma volta completa da pedivela.
• O pedal passará mais próximo do chão.
• Irá gerar um torque maior quando pedalar de pé – peso do ciclista multiplicado pelo comprimento do braço da pedivela -, mas com um deslocamento maior em cada rotação.

Ok. Habemus diferença.

De qualquer forma, a diferença é muito pequena, de difícil percepção – cerca de 3% -. Medidas mais significativas como relação de marcha – uns 12% de diferença de uma marcha para outra – ou calibragem dos pneus acabam mascarando alguma vantagem para um ciclista não profissional. A grosso modo, pode-se recomendar pedivelas maiores para pessoas maiores e passar para a próxima dificuldade que é encontrar a peça à venda do jeito que se deseja.

Hoje em dia é fácil encontrar um rolamento. Estão em todos os meios de transportes e máquinas que se possam imaginar. São fabricados em todos os cantos do mundo e em lojas especializadas é possível encontrá-los em praticamente todas as medidas que se possa imaginar. Isso nos deixa com a errônea impressão que estes itens são simples e fáceis de fabricar.

Na verdade, rolamentos representam uma espécie de Santo Graal da mecânica: sem eles, tudo que possui movimento seria mais complicado e menos eficiente. Assim sendo, precisam ser fabricados com extrema precisão, tendo em vista ainda as enormes cargas que suportam.

E afinal, o que são?

O conceito é relativamente simples. Colocar elementos circulares (esferas ou rolos) entre superfícies que tenham movimentos relativos. Em geral um eixo girante dentro de um apoio.

Rolamentos. Essa é a ideia geral.
Fonte: emeraldinsight.com

Porém a área matemática de uma esfera em contato com um plano é zero (um ponto). Na prática há uma pequena deformação e ao invés de zero a área é apenas muito pequena. Como pressão/tensão é dada por força dividida pela área, uma força aplicada em uma pequena área resulta em tensões enormes. E este é uma das razões do primeiro desafio de um sistema rolamentado: Material.

Material

O aço que compõe as pistas (anéis do rolamento) e as esferas não pode ser um aço comum. Em geral o aço usado em rolamentos é uma liga bastante nobre (SAE 52100) que possui tensão de escoamento na ordem de 2GPa. Isso é cerca de 10 vezes mais que um aço comum. Para isso além de usar um aço nobre é preciso também rigorosos tratamentos térmicos (têmpera, recozimento, etc)

Precisão Dimensional

Esse é outro desafio. Não se pode ter um rolamento travado e tampouco um que apresente folga já quando novo. Também não pode gerar vibrações. As especificações de precisão são bastante elevadas e bem longe do visível a olho nu.

Tanta qualidade para um único objetivo: Ser esquecido. Um rolamento de boa qualidade e bem dimensionado vai funcionar bem por muito tempo – muitas vezes durante toda a vida útil do equipamento, sem ser substituído – fazendo com que o usuário nem se lembre que há tanta tecnologia e desenvolvimento escondidos em algum lugar. E se falando em eficiência e atrito logo pensa-se em bicicleta.

Rolamentos e Bicicletas

Falando de Bicicleta, onde cada Watt de potência é precioso, encontramos uma variedade de juntas rolamentadas. Caixa de direção, movimento central e é claro, nas rodas. Comumente vemos juntas rolamentadas de contato angular, ou seja, ao invés de pistas paralelas vemos cones. Isto ocorre pelo tipo de esforço a qual ele está sujeito. Uma carga que é a composição de força axial com radial.

Rolamento aberto da popular Chin Haur

No mundo da bicicleta não existe um padrão entre usar rolamentos fechados ou abertos (bacias e esferas soltas). Existe uma tendência de que rolamentos abertos sejam mais baratos e mais leves, o que torna a aplicação mais adequada para bicicletas além de permitir a regulagem do aperto e eliminar folgas que surgem com o uso. Mas a máxima ainda permanece a mesma.

Rolamento fechado, não tão popular mas da mesma Chin Haur

Um rolamento bem construído e calculado não deve apresentar problemas. No caso de bicicletas onde a carga é extremamente baixa e o uso é pouco frequente – diferente de uma máquina industrial que gira 24 horas por dia 7 dias por semana – é possível que o sistema dure algumas décadas e seja trocado por motivo de obsolescência e não por vida útil, como é o caso dos cubos para cassetes de 7v, que já possuem 20 anos e são trocados (ainda funcionando) por cubos de 8/9/10v.

Acaba-se encontrando mais falhas em juntas rolamentadas (bacias e esferas ou rolamentos fechados) por motivos não relacionados ao funcionamento. Dentre os motivos está:

• oxidação: aços de alta dureza possuem mais carbono e são mais sujeitos a oxidação devido a entrada de água por lavagem com alta pressão / submersão / vedação ineficaz;
• abertura para manutenção: muitíssimas vezes desnecessário, o desmonte para substituição de graxas e esferas por outras fora das especificações e apertos incorretos.

Pelos motivos apresentados, se preocupar com as vantagens e desvantagens de sistemas abertos ou fechados tem menos valor do que ler o manual do fabricante. Seguindo direito as instruções muito provavelmente irá ser trocado por um modelo mais moderno antes de apresentar problemas.